算法入门

¶时间复杂度

¶大O时间复杂度

常见复杂度

复杂度术语

O(1) 常数阶

O(log(n)) 对数阶

O(n) 线性阶

O(nlog(n)) 对数阶

O(2^n) 指数阶

O(n!) 阶乘阶

O(n^k) k次方阶

复杂度	术语
O(1)	常数阶
O(log(n))	对数阶
O(n)	线性阶
O(nlog(n))	对数阶
O(2^n)	指数阶
O(n!)	阶乘阶
O(n^k)	k次方阶

其中将O(2^n)和O(n!)称为非多项式量级,该类问题就是NP问题
图像如下,来源bigocheatsheet

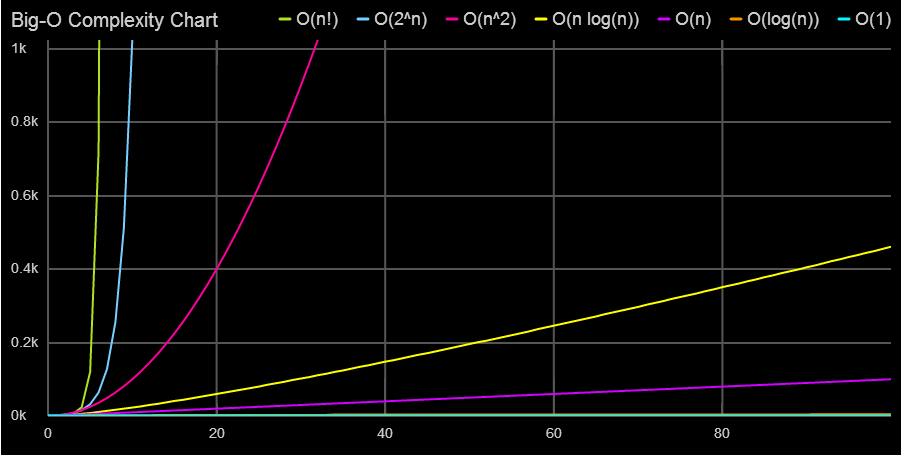
相关问题

对数阶以2为底

1	任意对数都可以转化为以2为底,log3 n=log32 * log2 n,可以看作O(Clogn)

O(m+n)、O(m*n)

加法原则:当多个复杂度堆叠时,若可以判断不同部分的数量级时,可使用大的替代整体,否则相加计算
乘法原则: T1(m)*T2(n) = O(f(m) * f(n))。

¶其他时间复杂度

最好,最坏时间复杂度
如二叉树的最坏时间复杂度为(O(n))即链表
平均时间复杂度
如在长度为n的数组,遍历寻找元素x,有n+1中情况,0---n-1位置以及不存在,则有n+1中情况,平均时间复杂度即每种情况平均花费的时间
其平均时间复杂度为 $$\frac{1+2+…+n+n}{n+1}=\frac{n(n+3)}{2(n+1)}$$,可以简化看作O(n)
将上述加入概率,假设元素存在为 1/2,元素在任意位置存在为1/n,可以得知每个位置出现的可能性为1/2n,则期望复杂度为$$1\times\frac{1}{2n}+2\times\frac{1}{2n}+…+n\times\frac{1}{2n}+n1\times\frac{1}{2}=\frac{3n+1}{4}$$ ,该值便是加权平均时间复杂度

均摊时间复杂度

例子


// array表示一个长度为n的数组
// 代码中的array.length就等于n
int[] array = new int[n];
int count = 0;

void insert(int val) {
   if (count == array.length) {
      int sum = 0;
      for (int i = 0; i < array.length; ++i) {
         sum = sum + array[i];
      }
      array[0] = sum;
      count = 1;
   }

   array[count] = val;
   ++count;
}

计算其时间平均时间复杂度为$$1*\frac{1}{n+1}+1*\frac{1}{n+1}+…+n*\frac{1}{n+1}+n*\frac{1}{n+1}=O(1)$$
最好时间复杂度为:$$O(1)$$
最坏时间复杂度为:$$O(n)$$
在该例子中可以将最后出现的O(n)操作均摊到每一次的O(1)操作上,那么可以理解均摊时间复杂度就是特殊的平均时间复杂度

¶线性表

简单来说数组,队列,栈,链表都是线性表,可以集中来分析插入,删除操作的复杂度,以及其方式

¶数组

插入操作

插入操作最差时间复杂度: O(n),平均时间复杂度 $$\frac{1+2+…+n}{n}=O(n)$$
当插入操作的目标数组并非要保持有序,可将插入位置元素挪到队尾,然后插入,则时间复杂可视为O(1)
插入操作
1
2
3
4
5
void insert(T e,int index) {
array[count-1] = array[index];
array[index] = e;
count++;
}
删除操作
可以采取标记删除,当数组容量不够时再进行删除并扩容